Test1 Review Material

Below are resources to help you practice and prepare for the tests in this course Test 1 will cover the material covered in Chapter 3 of this textbook.

Test Instructions

Below are the general instructions for all tests

You will get a chance to retake this. Your highest score counts toward your final grade.
Follow the guidance for each part and show all work for full credit.
Non-graphical calculators are allowed.
One page (two sides) of handwritten (or font size 8) notes are allowed.
The equation sheet from the textbook is included as part of the test pack (it doesn’t count as note pages)

Test 1 Spring 2025

Short-Answer Questions (20 points)

(4 pts) Explain how to test if a limit exists at a point on a function.
(4 pts) What is the difference between secant and tangent lines?
Explain using a sketch and how they relate to rates of change.
(4 pts) Identify a scenario where a function has a sharp corner or cusp and explain why the derivative does not exist there.
Include sketches.
(4 pts) What do the points where \(f'(x)=0\) represent on the graph of \(f(x)\)?
Include a sketch in your answer.
(4 pts) List the conditions required for a function to be differentiable at a point.
How do you test for these two conditions?

Problems (30 points)

Problem 1

Let \(f(x)=10x^{2}+e^{x}\).

(3 pts) Find the average velocity on the interval \([2,6]\).
(3 pts) Estimate, using the limit definition of the derivative, the instantaneous velocity at \(x=4\).

Problem 2

Using the limit definition of the derivative, let \(f(x)=x^{2}-4x\).

(3 pts) Find an expression for \(f'(x)\).
(2 pts) Find the derivative at \(x=3\).
(3 pts) Find the equation of the tangent line at \(x=3\).
(2 pts) Using \(f'(x)\), determine where the rate of change of \(f(x)\) is zero.
(2 pts) Explain how you would adapt the limit definition of a first derivative to find the second derivative.
(Do not actually compute \(f''(x)\).)
(2 pts) In words, what does the second derivative mean?

Problem 3

The graph of a function \(h(x)\) is shown below. Use it to answer the questions.

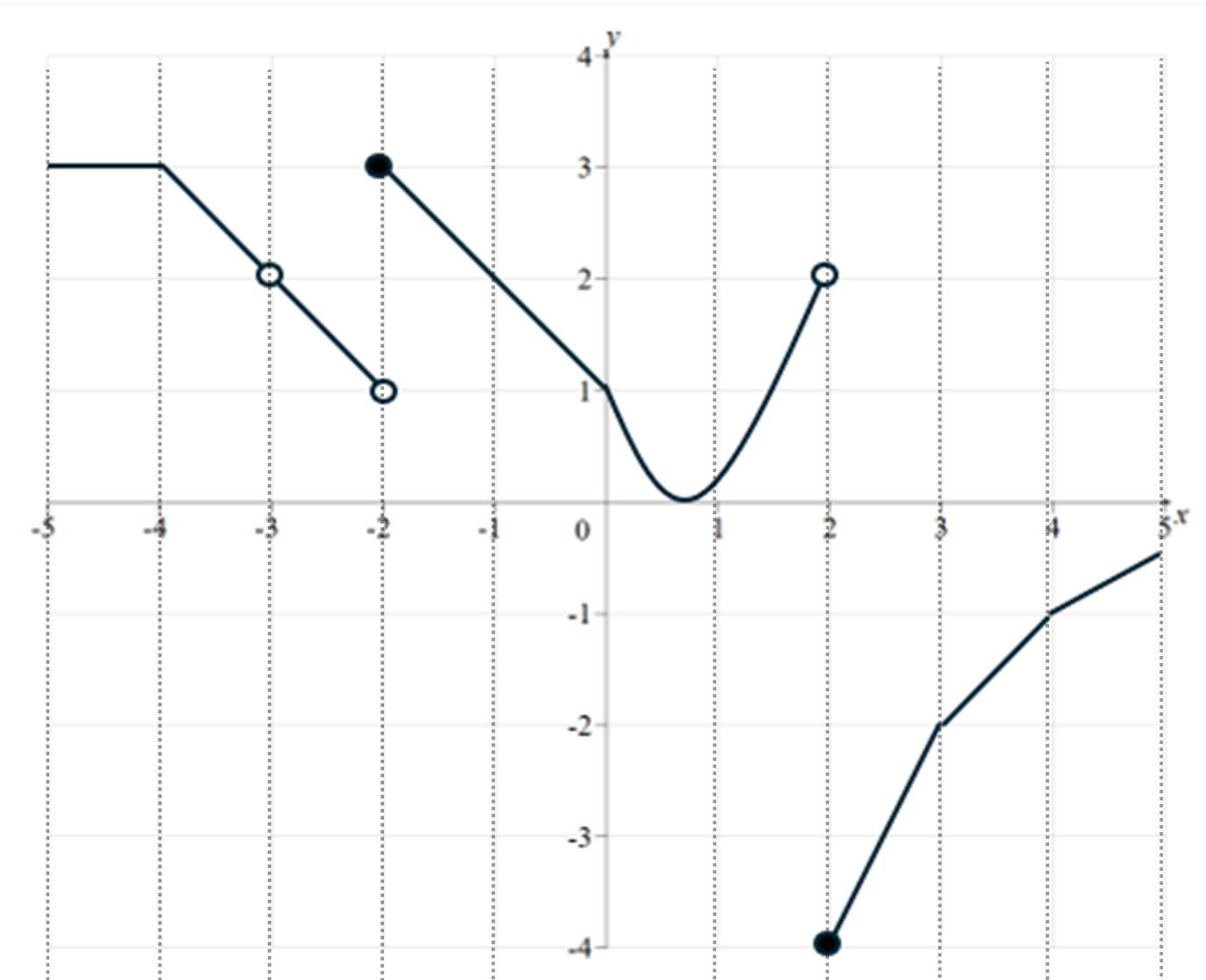
(2 pts) Identify all points where \(h(x)\) has no limit. Explain why.
(2 pts) Identify all points where \(h(x)\) is not continuous. Explain why.
(2 pts) Identify all points where \(h(x)\) is not differentiable. Explain why.
(4 pts) Roughly sketch the derivative \(h'(x)\).

Test 1 Spring 2025 Retake

Short-Answer Questions (20 points)

(4 pts) Describe how to determine whether a limit exists at a point using left-hand and right-hand limits.
Illustrate with a simple example.
(4 pts) Compare and contrast a secant line and a tangent line.
How are they used to estimate change?
Use a sketch to support your explanation.
(4 pts) Give an example of a function with a cusp or corner, and explain why the derivative is undefined at that point.
Include a sketch of the graph.
(4 pts) Explain the meaning of the points where the derivative of a function is zero.
How can you identify them visually on a graph?
(4 pts) State and explain the two main conditions required for a function to be differentiable at a point.
How would you test each condition?

Problems (30 points)

Problem 1

Let \(g(x) = 7x^2\).

(3 pts) Compute the average rate of change on the interval \([1,4]\).
(3 pts) Estimate the instantaneous rate of change at \(x = 2\) using the limit definition.

Problem 2

Let \(f(x) = x^2 + 2x\). Using the limit definition:

(3 pts) Derive the formula for \(f'(x)\).
(2 pts) Calculate the derivative at \(x = -1\).
(3 pts) Write the equation of the tangent line to \(f(x)\) at \(x = -1\).
(4 pts) Briefly describe how the limit definition could be used to find the second derivative.
Find an expression for \(f''(x)\).
(2 pts) Explain what the second derivative tells you about the behavior of the function.

Problem 3

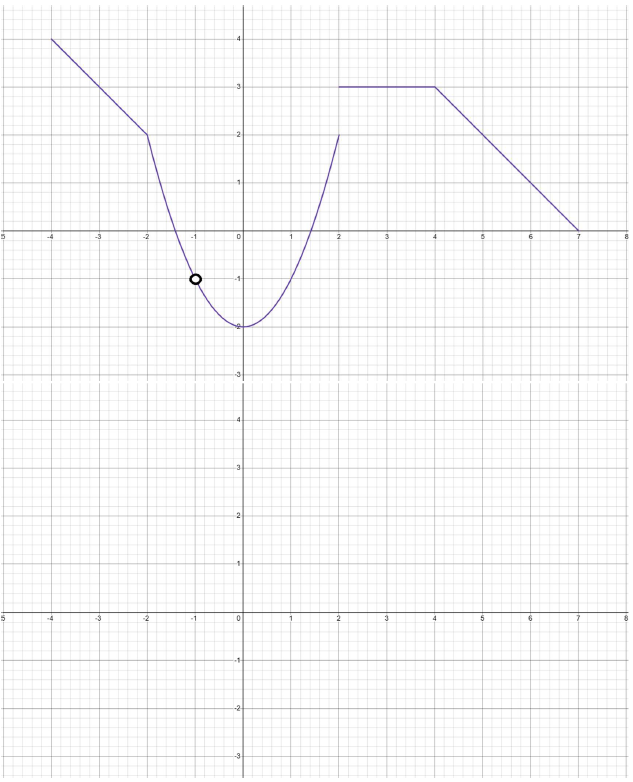
The graph of the function \(r(x)\) is shown below.

(2 pts) List all \(x\)-values where \(r(x)\) has no limit. Explain.
(2 pts) List all points where \(r(x)\) is not continuous. Explain why.
(2 pts) Identify all points where \(r(x)\) is not differentiable. Provide reasons.
(4 pts) Sketch a graph of the derivative \(r'(x)\), based on the shape of \(r(x)\).

Test 1 Winter 2025

Short-Answer Questions (24 points)

(3 pts) Provide an example (with a sketch) of a limit that does not exist and explain why it fails to exist.
(3 pts) What is the difference between average velocity and instantaneous velocity?
Explain using their equations.
(3 pts) How is the slope of a tangent line related to instantaneous rate of change?
Use a sketch in your answer.
(3 pts) Identify two scenarios where a function is not differentiable at a point, and provide examples (sketches) for each.
(3 pts) What does it mean for the left-hand and right-hand limits of the derivative of a function at a point \(a\) to be unequal?
(3 pts) What do the points where \(f'(x) = 0\) represent on the graph of \(f(x)\)?
Include a sketch in your answer.
(3 pts) How is the second derivative \(f''(x)\) related to \(f'(x)\) and the original function \(f(x)\)?
(3 pts) What is required for a function’s derivative to exist at all points?

Problems (26 points)

Problem 1

Let \(s(t) = 16t^2 + e^t\).

(3 pts) Find the average velocity on the interval \([1, 10]\).
(3 pts) Estimate the instantaneous velocity at \(t = 5\).

Problem 2

Using the limit definition of the derivative, let \(f(x) = x^2 + 3x\).

(3 pts) Find an expression for \(f'(x)\).
(2 pts) Find the derivative at \(f'(2)\).
(3 pts) Find the equation of the tangent line at \(x = 2\).
(2 pts) Using \(f'(x)\), determine where the rate of change of \(f(x)\) is zero.

Problem 3

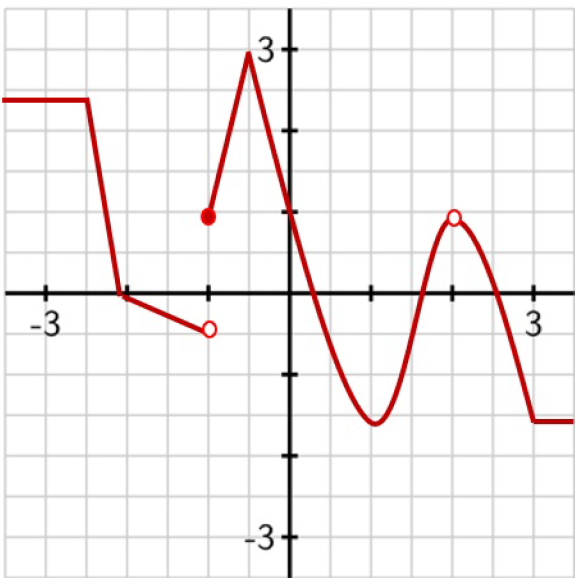
The graph of a function \(g(x)\) is shown below. Use it to answer the following questions.

(2 pts) Identify all points where \(g(x)\) has no limit. Explain why.
(2 pts) Identify all points where \(g(x)\) is not continuous. Explain why.
(2 pts) Identify all points where \(g(x)\) is not differentiable. Explain why.
(4 pts) Roughly sketch the derivative \(g'(x)\).

Practice Workbook: Limits, Continuity, and Derivatives

These questions align with Test 1 topics: limits, continuity, differentiability, tangent lines, and the limit definition of the derivative.

Use the sketch and notes spaces to reason before you compute.

Short-Answer Practice

Limits and Continuity

1. What does it mean for \(\lim_{x \to a} f(x)\) to exist?
Describe in words using the idea of left-hand and right-hand limits.

Notes:

2. Explain the conditions under which a limit can fail to exist.
Sketch simple example.

Sketch:

3. Give an example of a function where the limit exists but the function is not continuous at that point.
Explain why continuity fails.

Notes:

4. State the three conditions for continuity at a point.
Explain how to test each condition in practice.

Notes:

Rates of Change and Tangent Lines

5. Explain the relationship between a secant line and an average rate of change.

Notes:

6. How is a tangent line related to instantaneous rate of change?
Sketch a simple example showing both on the same graph.

Sketch:

7. What does a horizontal tangent line tell you about the behavior of a function?
Give an example in words or a sketch.

Notes:

8. How can the slope of a tangent line be negative even if the function’s output values are positive?

Notes:

Differentiability and Corners

9. State the two conditions a function must satisfy to be differentiable at a point.

Notes:

10. Give two examples of where a function might fail to be differentiable
(e.g., a sharp corner or a cusp).

Sketch:

11. How can a function be continuous but not differentiable?
Give an example.

Notes:

12. How can a you test to see if a function is smooth?
Give an example.

Notes:

Derivatives and Interpretation

13. Write the limit definition of the derivative.
Explain what each term represents.

Notes:

14. What does it mean when \(f'(x) = 0\)?
Sketch a function that has at least two such points.

Sketch:

15. Describe what information the second derivative provides about the function.
Include a real-world example.

Notes:

16. Explain how to find the equation of the tangent line at a point.

Notes:

17. What is the difference between average velocity and instantaneous velocity?
Write their respective equations.

Notes:

Problem Practice

A. Limits and Continuity

1. Evaluate the following limits:
a. \(\lim_{x \to 3} \frac{x^2 - 9}{x - 3}\)
b. \(\lim_{x \to 0} \frac{\sin(5x)}{x}\)
c. \(\lim_{x \to 2^-} \frac{|x - 2|}{x - 2}\)

2. For the piecewise function

\[ f(x) = \begin{cases} 2x + 3, & x < 1 \\ 5, & x = 1 \\ x^2 + 1, & x > 1 \end{cases} \]

Determine if \(f(x)\) is continuous at \(x = 1\).
Determine if \(f(x)\) is differentiable at \(x = 1\).

3. Sketch a function that is:
- Continuous everywhere but not differentiable at \(x = 2\).
- Discontinuous but with both left and right limits existing.

Sketch:

B. The Limit Definition of the Derivative

4. Using
\[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}, \] find \(f'(x)\) for:
a. \(f(x) = 3x^2 - 4x + 1\)
b. \(f(x) = \frac{1}{x}\)
c. \(f(x) = \sqrt{x}\)

5. Compute \(f'(a)\) using the definition for \(f(x) = x^2 + 2x\).

6. Find the equation of the tangent line to \(f(x) = x^2 + 2x\) at \(x = 1\).

C. Average and Instantaneous Rate of Change

7. Let \(s(t) = 2t^2 + 5t\).
a. Find the average velocity from \(t = 0\) to \(t = 4\).
b. Find the instantaneous velocity at \(t = 3\).
c. Interpret both values.

8. A population grows according to \(P(t) = 200e^{0.03t}\).
a. Find the average growth rate from \(t = 0\) to \(t = 10\).
b. Estimate the instantaneous growth rate at \(t = 5\).

9. A falling object has position \(s(t) = 100 - 4.9t^2\).
a. Find the average velocity from \(t = 0\) to \(t = 2\).
b. Find the instantaneous velocity at \(t = 2\).
c. Explain what these results mean physically.

D. Tangent Lines and Derivative Applications

10. For \(f(x) = x^3 - 2x + 1\):
a. Find \(f'(x)\).
b. Determine where \(f'(x) = 0\).
c. Classify each as a local max, min, or neither.

11. Write the equation of the tangent line to \(f(x) = \sin(x)\) at \(x = \pi/4\).

12. Find the tangent line to \(f(x) = e^x\) at \(x = 0\), and sketch both \(f(x)\) and the tangent.

E. Graphical Reasoning

13. The graph of \(f(x)\) has corners at \(x = -2\) and \(x = 3\).
a. At which points is \(f'(x)\) undefined?
b. Sketch a rough graph of \(f'(x)\).

14. Given a graph of \(f'(x)\):
a. Identify where \(f(x)\) is increasing or decreasing.
b. Identify where \(f(x)\) has local maxima or minima.
c. Sketch a possible \(f(x)\).

15. A graph of \(g(x)\) has horizontal tangents at \(x = 0\) and \(x = 4\).
What can you infer about the shape of \(g(x)\)?

Sketch:

F. Second Derivatives and Motion

16. For \(f(x) = x^3 - 3x^2 + 2\):
a. Find \(f'(x)\) and \(f''(x)\).
b. Identify where \(f(x)\) is concave up/down.
c. Find inflection points.

17. Suppose \(s(t) = t^3 - 6t^2 + 9t\).
a. Find velocity \(v(t)\) and acceleration \(a(t)\).
b. Find when the particle is at rest.
c. Determine when it’s speeding up or slowing down.

18. For \(f(x) = e^{-x^2}\):
a. Compute \(f'(x)\) and \(f''(x)\).
b. Explain what the signs of \(f'(x)\) and \(f''(x)\) tell you about the graph.

G. Mixed Concept Practice

19. Give an example of a function that:
- Has a limit at a point but is not defined there.
- Is defined at a point but the limit does not exist there.

20. Sketch a function where \(f'(x) = 0\) at two points and \(f'(x) > 0\) on one interval, \(f'(x) < 0\) on another.

21. In your own words, explain how derivatives connect graphs, algebra, and real-world change.

Notes: