Chapter 10 Derivative Rules - Workbook
10.1 Learning Objectives — Derivative Rules
By the end of this chapter, you should be able to:
- Read mathematical expressions as instructions and decompose a function into sums, constants, powers, products, quotients, and compositions.
- Apply basic rules — constant, power, constant multiple, sum/difference, \(e^x\), \(\ln x\), \(\sin x\), \(\cos x\) — to differentiate common terms without reverting to limits.
- Use the product, quotient, and chain rules to differentiate functions built from multiple changing parts, showing clear intermediate steps and correct notation.
- Select the right rule(s) for a given function by identifying its top-level structure and any nested “inside–outside” relationships.
- Interpret derivatives in context, explaining what a computed rate of change means for an environmental quantity (e.g., pollutant concentration, biomass, streamflow).
- Check and simplify results, factoring, combining like terms, and performing quick reasonableness checks (units, signs, limiting behavior).
- Communicate with multiple notations — prime, Leibniz, and operator — and translate between them accurately.
- Diagnose common errors, such as forgetting the inner derivative or misusing product vs. chain rule, and correct them using structured reasoning or unit checks.
Success looks like:
Given a new environmental model, you can:
- Identify which derivative rules apply,
- Compute \(f'(x)\) cleanly, and
- Explain in words what that derivative tells you about how the system is changing.
10.2 Activity: Reading Math as Instructions — The Derivative of a Constant
Not all functions change. A constant function is perfectly flat — no growth, no decline, no change over time or space.
The derivative gives us a way to prove that this lack of change equals a slope of zero.
10.2.1 Step 1: Read the Expression Aloud
Prompt:
Read this equation aloud and explain what each part is telling you to do:
\[ \frac{d}{dx}(c) = 0 \]
| Symbol / Term | What It Tells You To Do |
|---|---|
| \(\frac{d}{dx}\) | |
| \(c\) | |
| \(= 0\) |
Notes:
10.2.2 Step 2: Translate to a Step-by-Step Recipe
Activity:
In your own words, describe what the rule for a constant tells you to do.
- Recognize that the function’s value never changes — it’s constant for all \(x\).
- The “rate of change” or “slope” is therefore zero everywhere.
- When you apply the derivative operator \(\frac{d}{dx}\), the output is \(0\).
Now apply this to three examples:
| Function \(f(x)\) | What It Represents | Derivative \(f'(x)\) |
|---|---|---|
| \(f(x) = 7\) | Constant value | |
| \(f(x) = -12\) | Constant offset | |
| \(f(x) = 3.14\) | Physical constant |
Notes:
10.2.3 Step 3: Deriving the Rule from the Limit Definition
We can confirm this result directly from the limit definition of a derivative:
\[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \]
If \(f(x) = c\) (a constant), then:
\[ f'(x) = \lim_{h \to 0} \frac{c - c}{h} = \lim_{h \to 0} \frac{0}{h} = 0 \]
Because the numerator is always zero, the slope — the rate of change — is zero everywhere.
In words: “When nothing changes, the rate of change is zero.”
10.2.4 Step 4: Apply to Environmental Contexts
Practice:
For each situation, identify whether the derivative (rate of change) would be zero or nonzero.
| Scenario | Description | Is the Derivative Zero? | Why? |
|---|---|---|---|
| A lake’s surface area remains 10 km² for 10 years | |||
| Atmospheric CO₂ remains steady at 420 ppm for one month | |||
| Soil temperature remains constant throughout the day |
Now write one more realistic example where a quantity stays constant in your field (e.g., hydrology, forestry, marine science).
Notes:
10.3 Activity: Reading Math as Instructions — The Power Rule
Mathematics is a language of instructions.
When you see a formula like the Power Rule, you’re not just seeing symbols — you’re seeing a procedure that tells you what to do and how each step transforms the function.
10.3.1 Step 1: Read the Expression Aloud
Prompt:
Read this equation aloud and explain what each part is asking you to do:
\[ \frac{d}{dx}\big(x^n\big) = n x^{n-1} \]
| Symbol / Term | What It Tells You To Do |
|---|---|
| \(\frac{d}{dx}\) | |
| \(x^n\) | |
| \(n\) | |
| \(x^{n-1}\) |
Notes:
10.3.2 Step 2: Translate to a Step-by-Step Recipe
Activity (Think–Pair–Share):
In your own words, write the recipe the Power Rule gives you for differentiating \(x^n\):
- Look at the exponent \(n\).
- Multiply the whole expression by that exponent.
- Subtract one from the exponent.
- Keep the base \(x\) the same.
Now apply this recipe to three quick examples:
| Function \(f(x)\) | Your Steps | Derivative \(f'(x)\) |
|---|---|---|
| \(x^2\) | ||
| \(x^5\) | ||
| \(x^{-3}\) |
Notes:
10.3.3 Step 3: Deriving the Power Rule from the Limit Definition
Let’s see how the Power Rule comes directly from the limit definition of a derivative.
We start with:
\[ f'(x) = \lim_{h \to 0} \frac{(x+h)^n - x^n}{h} \]
We expand \((x+h)^n\) using the Binomial Theorem:
\[ (x + h)^n = x^n + n x^{n-1}h + \frac{n(n-1)}{2}x^{n-2}h^2 + \cdots + h^n \]
Substitute this expansion into the limit expression:
\[ f'(x) = \lim_{h \to 0} \frac{\big(x^n + n x^{n-1}h + \frac{n(n-1)}{2}x^{n-2}h^2 + \cdots + h^n\big) - x^n}{h} \]
Simplify the numerator — the \(x^n\) terms cancel:
\[ f'(x) = \lim_{h \to 0} \frac{n x^{n-1}h + \frac{n(n-1)}{2}x^{n-2}h^2 + \cdots + h^n}{h} \]
Now factor out \(h\):
\[ f'(x) = \lim_{h \to 0} \Big( n x^{n-1} + \frac{n(n-1)}{2}x^{n-2}h + \cdots + h^{n-1} \Big) \]
As \(h \to 0\), all terms containing \(h\) vanish, leaving only:
\[ \boxed{f'(x) = n x^{n-1}} \]
That’s the Power Rule — it’s the simplified result of the limit definition.
10.4 Activity: Reading Math as Instructions — The Constant Multiplier Rule
The Constant Multiplier Rule tells us how constants behave when we take derivatives.
It’s the mathematical version of saying: “Scaling a process doesn’t change how fast it changes — only by how much.”
10.4.1 Step 1: Read the Expression Aloud
Prompt:
Read this equation aloud and explain what each part is telling you to do:
\[ \frac{d}{dx}\big[c \cdot f(x)\big] = c \cdot f'(x) = c \cdot \frac{d}{dx}\big[f(x)\big] \]
| Symbol / Term | What It Tells You To Do |
|---|---|
| \(c\) | |
| \(f(x)\) | |
| \(f'(x)\) | |
| \(c \cdot f'(x)\) |
Notes:
10.4.2 Step 2: Translate to a Step-by-Step Recipe
Activity (Think–Pair–Share):
Describe the procedure this rule gives you in plain English.
- Identify the constant \(c\).
- Differentiate the variable part \(f(x)\) as usual.
- Keep the constant \(c\) in front — it “comes along for the ride.”
- Multiply \(c\) by the derivative \(f'(x)\).
Now apply this recipe to three examples:
| Function \(f(x)\) | Constant \(c\) | Derivative \(f'(x)\) |
|---|---|---|
| \(5x^3\) | ||
| \(-2x^4\) | ||
| \(7\) |
Notes:
10.4.3 Step 3: Deriving the Rule from the Limit Definition
We can prove the rule using the limit definition of a derivative:
\[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \]
For a constant multiple \(g(x) = c \cdot f(x)\):
\[ g'(x) = \lim_{h \to 0} \frac{c \cdot f(x+h) - c \cdot f(x)}{h} \]
Factor out the constant \(c\):
\[ g'(x) = c \cdot \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \]
Recognize that the remaining limit is just \(f'(x)\):
\[ \boxed{g'(x) = c \cdot f'(x)} \]
That’s the Constant Multiplier Rule — the constant stays the same, while the variable part changes according to its own derivative.
10.4.4 Step 4: Apply the Instructions to a Real Example
Practice:
Let \(f(x) = x^2\), and define \(g(x) = 3f(x)\).
- Identify the constant multiplier \(c\).
- Use the Power Rule to find \(f'(x)\).
- Apply the Constant Multiplier Rule.
- Simplify the result.
Interpretation:
If \(f(x)\) describes tree height over time, multiplying by 3 simply scales the entire process — the rate of growth is three times faster, but the shape of the change is identical.
Notes:
10.5 Activity: Reading Math as Instructions — The Sum and Difference Rules
When we add or subtract functions, each one still changes according to its own rule.
The Sum and Difference Rules tell us that differentiation distributes over addition and subtraction —
you can take the derivative of each part separately and then combine the results.
10.5.1 Step 1: Read the Expression Aloud
Prompt:
Read the following equations aloud and describe what they’re instructing you to do:
\[ \frac{d}{dx}\big[f(x) + g(x)\big] = f'(x) + g'(x) \]
\[ \frac{d}{dx}\big[f(x) - g(x)\big] = f'(x) - g'(x) \]
| Symbol / Term | What It Tells You To Do |
|---|---|
| \(f(x) + g(x)\) | |
| \(f'(x) + g'(x)\) | |
| \(f(x) - g(x)\) | |
| \(f'(x) - g'(x)\) |
Notes:
10.5.2 Step 2: Translate to a Step-by-Step Recipe
Activity (Think–Pair–Share):
Write the recipe the Sum and Difference Rules describe in your own words.
- Break the function into parts being added or subtracted.
- Take the derivative of each part individually.
- Keep the same operation (addition or subtraction) between them.
- Simplify the result.
Now apply this recipe to three quick examples:
| Function \(f(x)\) | Steps You’d Take | Derivative \(f'(x)\) |
|---|---|---|
| \(x^2 + 3x\) | ||
| \(4x^3 - 5x^2\) | ||
| \(2x^4 - 7x + 9\) |
Notes:
10.5.3 Step 3: Deriving the Rule from the Limit Definition
Let’s see how this rule arises from the limit definition of the derivative.
We start with: \[ h'(x) = \lim_{h \to 0} \frac{h(x+h) - h(x)}{h} \] and let \(h(x) = f(x) + g(x)\).
Then: \[ h'(x) = \lim_{h \to 0} \frac{[f(x+h) + g(x+h)] - [f(x) + g(x)]}{h} \]
Simplify: \[ h'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} + \lim_{h \to 0} \frac{g(x+h) - g(x)}{h} \]
Recognize each term as a derivative: \[ \boxed{h'(x) = f'(x) + g'(x)} \]
The same reasoning works for subtraction: \[ \boxed{\frac{d}{dx}[f(x) - g(x)] = f'(x) - g'(x)} \]
In short — differentiation distributes over addition and subtraction.
10.5.4 Step 4: Apply the Instructions to a Real Example
Practice:
Let \(f(x) = 3x^3 + 4x^2 - 10x\).
- Identify how many terms there are.
- Apply the derivative to each term using the Power Rule.
- Combine the results.
- Simplify your answer.
Notes:
10.5.5 Step 5: Visualize What’s Happening
Visualization Prompt:
Examine the graphs of \(f(x) = x^2\) and \(g(x) = x\).
Their sum \(f(x) + g(x)\) combines both shapes —
the derivative \(f'(x) + g'(x)\) describes how both rates of change add together at each point.
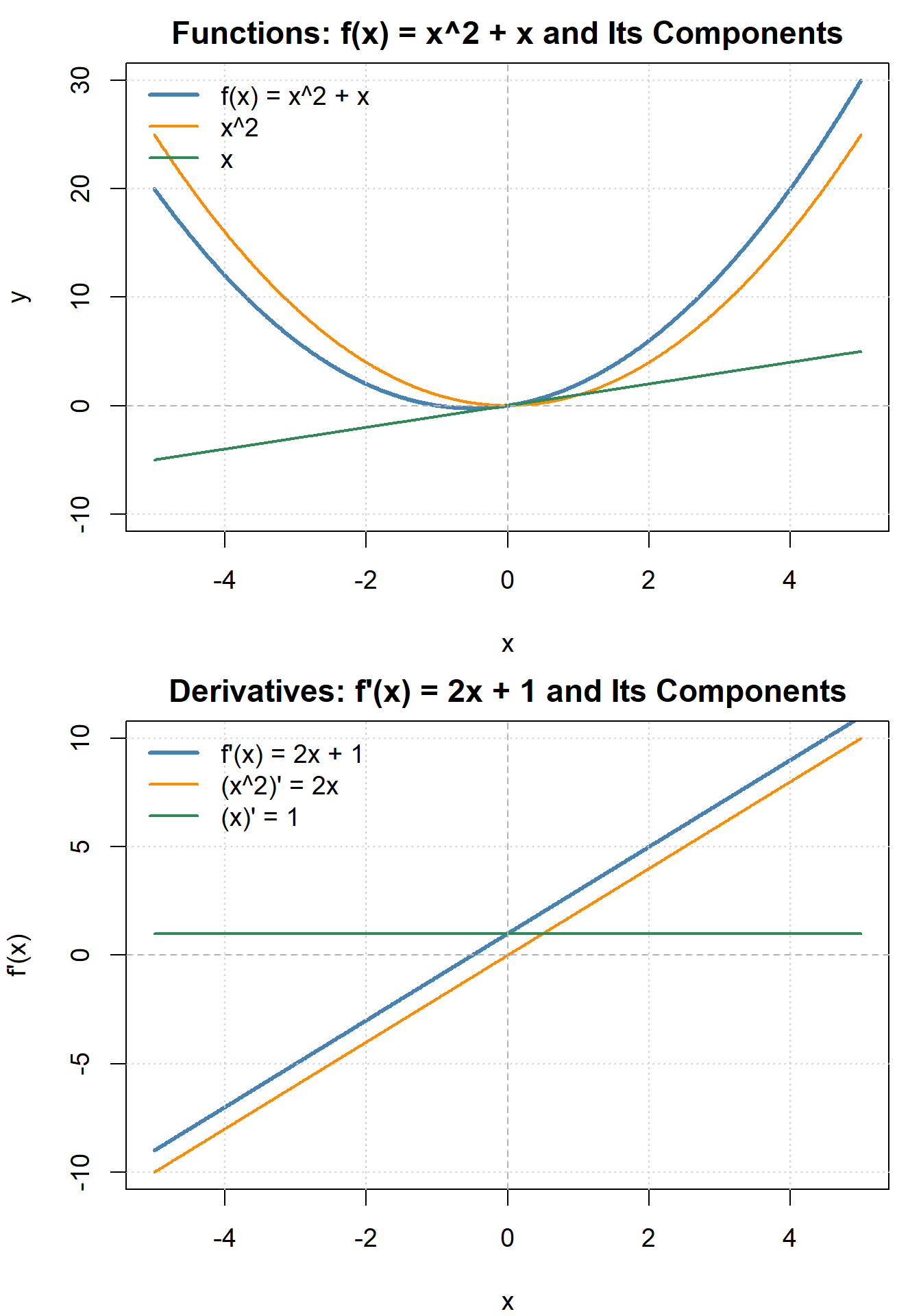
What do you notice about how the slopes of the two functions interact?
Notes:
10.6 Practice: Identifying and Applying Derivative Rules
Each of the following problems involves one or more of the basic derivative rules you’ve learned so far:
- Constant Rule: \(\frac{d}{dx}(c) = 0\)
- Constant Multiplier Rule: \(\frac{d}{dx}[c \cdot f(x)] = c \cdot f'(x)\)
- Power Rule: \(\frac{d}{dx}(x^n) = n x^{n-1}\)
- Sum/Difference Rule: \(\frac{d}{dx}[f(x) \pm g(x)] = f'(x) \pm g'(x)\)
For each function below:
- Identify which rule(s) apply.
- Write each step of differentiation clearly.
- Simplify your final answer.
- When possible, interpret what the derivative tells you about how the quantity is changing.
10.6.1 Problem 1
\[ f(x) = 7 \]
Tasks:
- Identify which rule applies.
- Explain why the derivative is zero.
Notes:
10.6.2 Problem 2
\[ f(x) = 5x^3 \]
Tasks:
- Identify which rule(s) apply.
- Compute \(f'(x)\).
- Interpret what happens to the rate of change when you multiply the function by 5.
Notes:
10.6.3 Problem 3
\[ f(x) = -2x^4 + 9x \]
Tasks:
- Identify all rules used.
- Compute \(f'(x)\).
- Check whether the derivative is positive, negative, or zero when \(x = 1\).
Notes:
10.6.4 Problem 4
\[ f(x) = 6x^2 - 8 \]
Tasks:
- Identify the constant, power, and constant multiplier rules as they appear.
- Compute \(f'(x)\).
- Which term disappears? Why?
Notes:
10.6.5 Problem 5
\[ f(x) = 3x^5 + 2x^2 - 10 \]
Tasks:
- Identify each rule used.
- Write out the derivative term by term.
- Simplify the final expression.
Notes:
10.6.6 Problem 6
\[ f(x) = -7x^{-3} \]
Tasks:
- Identify which rule(s) apply.
- Compute \(f'(x)\) using the Power Rule for negative exponents.
- How does the sign of the derivative compare to the original function?
Notes:
10.6.7 Problem 7
\[ f(x) = \frac{1}{4}x^4 - 9x^2 + 12 \]
Tasks:
- Identify the rules used for each term.
- Compute the derivative step-by-step.
- Simplify and factor the result if possible.
Notes:
10.6.8 Problem 8
\[ f(x) = 2(5x^3 - 4x) \]
Tasks:
- Identify which rule applies first (constant multiplier or power?).
- Apply the constant multiplier rule correctly.
- Expand and simplify \(f'(x)\).
Notes:
10.6.9 Problem 9
\[ f(x) = 4x^2 + 3x^{-1} - 7 \]
Tasks:
- Identify the power and constant rules used.
- Write each differentiation step.
- Discuss what happens to the derivative as \(x \to 0\).
Notes:
10.7 Workbook: Trigonometric Derivatives
Learning goals
- Recognize and apply the derivative rules for sine, cosine, and tangent.
- Visually connect a function’s graph to the shape of its derivative.
- Practice taking derivatives that require the chain rule with trig functions.
10.7.1 Visual Warm-Up: Sketch the derivatives\(\sin x\), \(\cos x\), \(\tan x\)
Prompt:
- For each top plot, sketch the derivative on the corresponding blank axes below.
- Where is the slope positive/negative/zero? Mark a few key points (e.g., where slope is zero or maximally positive/negative).
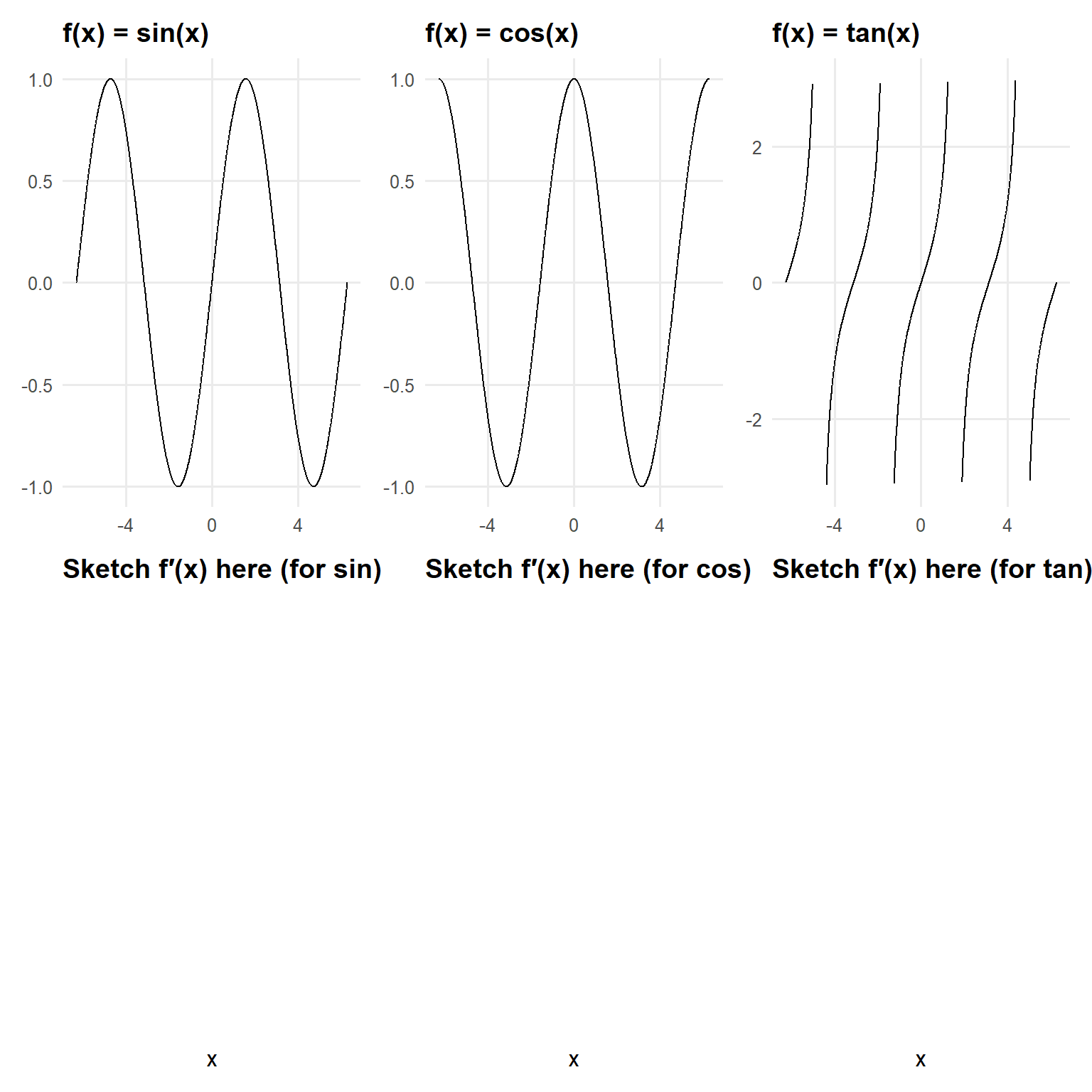
10.7.2 Trig Derivative Rules (for reference)
| Function | Derivative |
|---|---|
| \(\sin x\) | \(\cos x\) |
| \(\cos x\) | \(-\sin x\) |
| \(\tan x\) | \(\sec^2 x\) |
| \(\sec x\) | \(\sec x \tan x\) |
| \(\csc x\) | \(-\csc x \cot x\) |
| \(\cot x\) | \(-\csc^2 x\) |
And a reminder of some of the trig functions
| Function | Definition (in terms of sine and cosine) |
|---|---|
| \(\tan(x)\) | \(\dfrac{\sin(x)}{\cos(x)}\) |
| \(\sec(x)\) | \(\dfrac{1}{\cos(x)}\) |
| \(\cot(x)\) | \(\dfrac{\cos(x)}{\sin(x)}\) |
| \(\csc(x)\) | \(\dfrac{1}{\sin(x)}\) |
Notes:
- These are base identities. The ONLY when the trigonometric operator is x. In a week we’ll learn how to take the derivative of something that takes the form of \(sin(f(x))\)
10.7.3 Practice Problems: Trigonometric Derivatives
Use the derivative rules below to find each derivative.
Problem 1
Find the derivative of
\[
f(x) = 10\sin(x)
\]
Notes:
Solution
\[ f'(x) = 10\cos(x) \]Problem 2
Find the derivative of
\[
f(x) = -7\cos(x)
\]
Notes:
Solution
\[ f'(x) = -7[-\sin(x)] = 7\sin(x) \]Problem 3
Find the derivative of
\[
f(x) = 4\tan(x) - 2\csc(x)
\]
Notes:
Solution
\[ f'(x) = 4\sec^2(x) - 2[-\csc(x)\cot(x)] = 4\sec^2(x) + 2\csc(x)\cot(x) \]10.8 Workbook: Exponential and Logarithmic Derivatives
Learning goals
- Recognize and apply the derivative rules for exponential and logarithmic functions.
- Visually connect the function and its derivative through growth and decay patterns.
- Practice applying constant multiple and sum rules with exponential and logarithmic functions.
10.8.1 Visual Warm-Up: Sketch the derivatives of \(e^x\), \(a^x\), and \(\ln(x)\)
Prompt:
- For each top plot, sketch the derivative on the corresponding blank axes below.
- How does the derivative compare to the original function?
- Where is the rate of change the greatest?
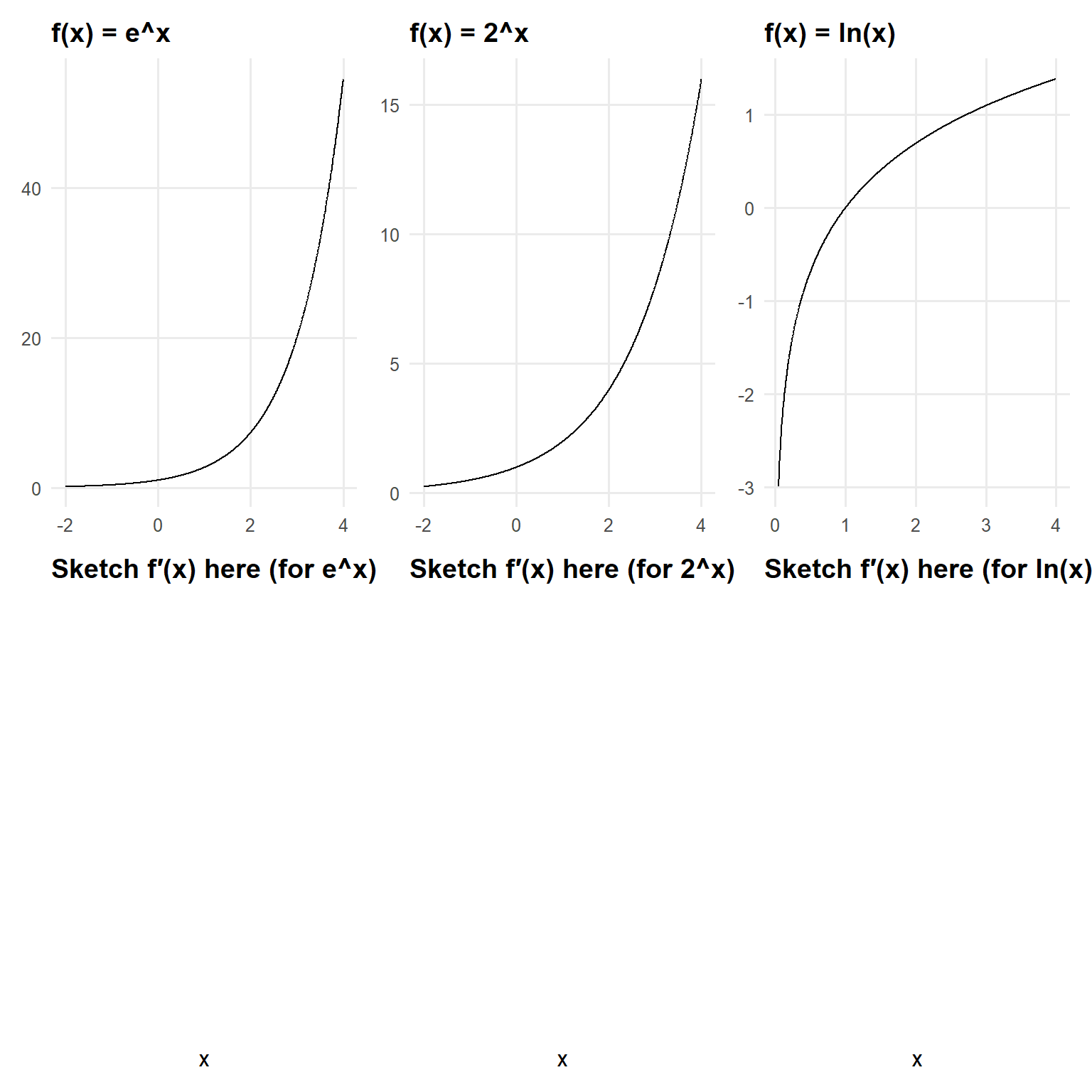
Exponential & Logarithmic Derivatives
| Function | Derivative |
|---|---|
| \(a^x\) | \(a^x \ln(a)\) |
| \(e^x\) | \(e^x\) |
| \(\log_a(x)\) | \(\dfrac{1}{x \ln(a)}\) |
| \(\ln(x)\) | \(\dfrac{1}{x}\) |
Notes:
- These are base identities, valid only when the exponent or argument is x (not another function).
Problem 1
Find the derivative of
\[
f(x) = 6e^x
\]
Notes:
Solution
\[ f'(x) = 6e^x \]Problem 2
Find the derivative of
\[
f(x) = 5 \cdot 3^x
\]
Notes:
Solution
\[ f'(x) = 5 \cdot 3^x \ln(3) \]Problem 3
Find the derivative of
\[
f(x) = 4\ln(x) - 2\log_{10}(x)
\]
Notes:
Solution
\[ f'(x) = 4\left(\frac{1}{x}\right) - 2\left(\frac{1}{x \ln(10)}\right) \]10.9 Reading Math Self Check
Learning goal:
Strengthen your ability to read mathematical notation and apply derivative rules that involve inner functions \(g(x)\).
10.9.1 Exponential and Logarithmic Rules (General Form)
| Function | Derivative |
|---|---|
| \(a^{g(x)}\) | \(g'(x)\, a^{g(x)} \ln(a)\) |
| \(e^{g(x)}\) | \(g'(x)\, e^{g(x)}\) |
| \(\log_a(g(x))\) | \(\dfrac{g'(x)}{g(x)\ln(a)}\) |
| \(\ln(g(x))\) | \(\dfrac{g'(x)}{g(x)}\) |
10.9.2 How to Use This Section
This section is meant to help you check your understanding — without step-by-step guidance.
Read each rule carefully, then apply it to the corresponding problem.
Problem 1 — Using \(a^{g(x)}\)
Rule reminder:
\[
\frac{d}{dx}\big[a^{g(x)}\big] = g'(x)\,a^{g(x)}\ln(a)
\]
Find the derivative of
\[
f(x) = 3^{2x}
\]
Notes:
Solution
Here \(a = 3\) and \(g(x) = 2x\), so \(g'(x) = 2\).\[ f'(x) = 2 \cdot 3^{2x} \ln(3) \]
Problem 2 — Using \(e^{g(x)}\)
Rule reminder:
\[
\frac{d}{dx}\big[e^{g(x)}\big] = g'(x)\,e^{g(x)}
\]
Find the derivative of
\[
f(x) = e^{5x - 1}
\]
Notes:
Solution
Here \(g(x) = 5x - 1\), so \(g'(x) = 5\).\[ f'(x) = 5e^{5x - 1} \]
Problem 3 — Using \(\log_a(g(x))\)
Rule reminder:
\[
\frac{d}{dx}\big[\log_a(g(x))\big] = \frac{g'(x)}{g(x)\ln(a)}
\]
Find the derivative of
\[
f(x) = \log_2(x^3 + 1)
\]
Notes:
Solution
Here \(a = 2\), \(g(x) = x^3 + 1\), and \(g'(x) = 3x^2\).\[ f'(x) = \frac{3x^2}{(x^3 + 1)\ln(2)} \]
Problem 4 — Using \(\ln(g(x))\)
Rule reminder:
\[
\frac{d}{dx}\big[\ln(g(x))\big] = \frac{g'(x)}{g(x)}
\]
Find the derivative of
\[
f(x) = \ln(4x^2 + 5)
\]
Notes:
Solution
Here \(g(x) = 4x^2 + 5\), so \(g'(x) = 8x\).\[ f'(x) = \frac{8x}{4x^2 + 5} \]
10.9.3 Reflection
- Which parts of the rule notation did you initially overlook?
- What helped you identify \(g(x)\) and \(g'(x)\) correctly?
- How does this process differ from using the simpler base forms like \(e^x\) or \(\ln(x)\)?
Key takeaway:
Being able to “read” and interpret symbolic rules like these is a core mathematical skill — it’s not just about memorization, but about recognizing structure and patterns across different functions.
10.10 Derivative Rule Practice
There are 4 sets of 5 questions. Each question has a function for which you must find the derivative. There is also a followup questions for each questions
Solutions for these five are hidden behind a password at the bottom (once you are done - ask one of us)
Derivative Applications (Set 1 of 4)
1. \(f(x)=8x^{5/2}-6x^{3/2}+4x^{1/2}\)
Follow-up: For \(x>0\), describe how the sign of \(f'(x)\) changes as \(x\) increases.
(Does the slope stay positive, become negative, or switch direction?)
Math Hint
Use the Power Rule: \(\frac{d}{dx}x^n = n x^{n-1}\).Each term keeps a positive coefficient, so think about how the powers affect growth.
Conceptual Phone a Friend
Differentiate each term and notice that as \(x\) grows, the higher-power term \(x^{3/2}\) grows fastest.That means the slope increases for large \(x\) but could be smaller near \(x=0\).
2. \(f(x)=5x^{-3}+2x^{-1/2}-7\)
Follow-up: What is the sign of \(f'(x)\) when \(x=0.5\)? Explain why.
Math Hint
Power Rule again. Don’t forget the negative signs that appear when differentiating negative exponents.Conceptual Phone a Friend
At small \(x\), terms with higher negative powers dominate because they “blow up.”Ask which derivative term—steeply negative or mildly negative—controls the overall direction of change.
3. \(f(x)=x^4-8x^2+16\)
Follow-up: Identify the points where the tangent line is horizontal.
Math Hint
Apply the Power Rule term-by-term; combine like terms neatly.You’ll get a polynomial you can factor.
Conceptual Phone a Friend
A “horizontal tangent” means the slope momentarily stops increasing or decreasing.Think of it as the peak or valley of the curve—places where growth pauses before reversing.
4. \(f(x)=2x^{1/3}-3x^{2/3}+4x^{5/3}\)
Follow-up: How does the derivative behave near \(x=0\)?
Math Hint
Be meticulous with fractional powers: \(x^{1/3}\), \(x^{2/3}\), \(x^{5/3}\).Subtract 1 from each exponent carefully.
Conceptual Phone a Friend
Negative exponents create division by small numbers.As \(x\to0\), imagine the graph’s slope stretching vertically — the function’s rate of change explodes rather than settling.
5. \(f(x)=9x^6-5x^3+1\)
Follow-up: What happens to the slope as \(x\to\infty\)?
Math Hint
Differentiate each term using the Power Rule.Keep coefficients exact; the highest power dictates long-term growth.
Conceptual Phone a Friend
For very large \(x\), the biggest power term outweighs all others.Picture a rocket—lower-order terms fade as the \(x^6\) term propels the slope steeply upward.
🔒 Answer Key (Questions 1 – 5)
Click to Unlock Solutions
1.
Derivative: \(f'(x)=20x^{3/2}-9x^{1/2}+2x^{-1/2}\).
Follow-up answer: For small \(x\), the \(2x^{-1/2}\) term dominates, so \(f'(x)\) is positive and large.
As \(x\) increases, \(20x^{3/2}\) eventually becomes dominant and positive as well, so the slope stays positive for all \(x>0\).
Thus \(f(x)\) is increasing on \((0,\infty)\).
2.
Derivative: \(f'(x)=-15x^{-4}-x^{-3/2}\).
Follow-up answer: At \(x=0.5\), both terms are negative and large in magnitude, so \(f'(0.5)<0\).
The function is decreasing there (the higher-order negative power dominates).
3.
Derivative: \(f'(x)=4x^3-16x=4x(x^2-4)\).
Follow-up answer: Horizontal tangents where \(f'(x)=0\): \(x=-2,\,0,\,2\).
4.
Derivative: \(f'(x)=\tfrac{2}{3}x^{-2/3}-2x^{-1/3}+\tfrac{20}{3}x^{2/3}\).
Follow-up answer: As \(x\to0^+\), the \(\tfrac{2}{3}x^{-2/3}\) term dominates (the most singular), so \(f'(x)\to +\infty\).
5.
Derivative: \(f'(x)=54x^5-15x^2\).
Follow-up answer: As \(x\to\infty\), the \(54x^5\) term dominates, so \(f'(x)\to+\infty\) (slope grows rapidly positive).
Derivative Applications (Set 2 of 4)
6. \(f(x)=x^{4}-x^{3}\)
Follow-up: Solve \(f'(x)=0\) and list all \(x>0\) where the tangent is horizontal.
Math Hint
Differentiate term-by-term: \((x^4)'=4x^3\), \((x^3)'=3x^2\).You’ll get \(f'(x)=4x^3-3x^2\). Factor out the largest common power of \(x\).
Conceptual Phone a Friend
Horizontal tangents occur where the slope is zero.A repeated factor like \(x^2\) means the graph “flattens” at that \(x\) (multiplicity \(>1\)) and may not change direction there.
7. \(f(x)=\sqrt{x}+\dfrac{3}{x^2}\)
Follow-up: Find \(f''(x)\).
Math Hint
Rewrite as powers: \(\sqrt{x}=x^{1/2}\) and \(3/x^2=3x^{-2}\).Differentiate once to get \(f'(x)=\tfrac{1}{2}x^{-1/2}-6x^{-3}\).
Differentiate again—each exponent decreases by 1 each time.
Conceptual Phone a Friend
You’re differentiating the derivative again to find how the slope \(f'(x)\) changes.Simplify your final expression to write \(f''(x)\) with clean coefficients and exponents.
8. \(f(x)=4x^{3/2}+7x^{-1/2}-5x\)
Follow-up: Does \(f'(x)\) change sign as \(x\) increases from \(0.1\) to \(10\)? Briefly justify.
Math Hint
Differentiate carefully: the derivative will have one positive-power term and two with exponents \(1/2\) and \(-3/2\).Evaluate the sign of \(f'(x)\) for a small \(x\) (e.g., \(0.1\)) and a large \(x\) (e.g., \(10\)).
Conceptual Phone a Friend
For tiny \(x\), the \(x^{-3/2}\) term dominates (very negative). For large \(x\), the \(x^{1/2}\) term dominates (positive).If a continuous derivative goes from negative to positive on an interval, it must cross zero somewhere in between.
9. \(f(x)=6x^{4}-9x^{1/2}+2x^{-1}\)
Follow-up: Which term dominates \(f'(x)\) for large \(x\)? For small \(x>0\)? State the sign in each case.
Math Hint
Differentiate and compare the exponents in \(f'(x)\).As \(x\to\infty\), highest positive power wins; as \(x\to0^+\), the most negative exponent wins.
Conceptual Phone a Friend
Dominance is about “who grows fastest.” Big positive powers explode for large \(x\); steep negative powers explode near zero.Use that to predict the sign of the slope in each regime.
10. \(f(x)=5x^{2/3}-3x^{1/3}+7\)
Follow-up: Compute \(f'(1)\). Then describe what happens to \(f'(x)\) as \(x\to0^+\).
Math Hint
Apply the fractional Power Rule carefully: \(\dfrac{d}{dx}x^{p} = p\,x^{p-1}\).Substitute \(x=1\) after you simplify \(f'(x)\).
Conceptual Phone a Friend
Near \(x=0^+\), terms like \(x^{-1/3}\) and \(x^{-2/3}\) can blow up.Decide which negative fractional power drives the behavior and whether it sends the slope toward \(+\infty\) or \(-\infty\).
🔒 Answer Key (Questions 6 – 10)
Click to Unlock Solutions
6.
Derivative: \(f'(x)=4x^{3}-3x^{2}=x^{2}(4x-3)\).
Follow-up answer: Roots at \(x=0\) (double root) and \(x=\tfrac{3}{4}\).
Since the prompt asks for \(x>0\), the horizontal tangent occurs at \(x=\tfrac{3}{4}\) (note: \(x=0\) is also a horizontal tangent but is not \(>0\)).
7.
Derivative: \(f'(x)=\tfrac{1}{2}x^{-1/2}-6x^{-3}\).
Second derivative: \(f''(x)=-\tfrac{1}{4}x^{-3/2}+18x^{-4}\).
8.
Derivative: \(f'(x)=6x^{1/2}-\tfrac{7}{2}x^{-3/2}-5\).
Follow-up answer: For small \(x\) (e.g., \(0.1\)), the \(-\tfrac{7}{2}x^{-3/2}\) term dominates \(\Rightarrow f'(x)<0\).
For large \(x\) (e.g., \(10\)), \(6x^{1/2}\) dominates \(\Rightarrow f'(x)>0\).
By continuity on \([0.1,10]\) (IVT), \(f'\) changes sign, so \(\exists\,c\in(0.1,10)\) with \(f'(c)=0\).
9.
Derivative: \(f'(x)=24x^{3}-\tfrac{9}{2}x^{-1/2}-2x^{-2}\).
Follow-up answer: As \(x\to\infty\), \(24x^{3}\) dominates \(\Rightarrow f'(x)>0\) (large positive).
As \(x\to0^+\), \(-2x^{-2}\) dominates \(\Rightarrow f'(x)\to-\infty\) (large negative).
10.
Derivative: \(f'(x)=\tfrac{10}{3}x^{-1/3}-x^{-2/3}\).
Follow-up answer: \(f'(1)=\tfrac{10}{3}-1=\tfrac{7}{3}>0\).
As \(x\to0^+\), the \(-x^{-2/3}\) term dominates, so \(f'(x)\to-\infty\).
Derivative Applications (Set 3 of 4)
11. \(f(x)=6\sin x-3\cos x+2\)
Follow-up: Explain why \(f'(x)=0\) has infinitely many solutions.
Math Hint
Differentiate using \((\sin x)'=\cos x\) and \((\cos x)'=-\sin x\).You’ll get a combination of sine and cosine—both periodic functions.
Conceptual Phone a Friend
Because sine and cosine repeat every \(2\pi\), any equation like\(A\cos x + B\sin x = 0\) will also repeat its zeros every period.
That’s why the slope \(f'(x)\) equals zero infinitely many times.
12. \(f(x)=4x^2+3\sin x\)
Follow-up: At \(x=\tfrac{\pi}{2}\), which term contributes more to \(f'(x)\)?
Math Hint
Differentiate to get a polynomial term and a cosine term. Then plug in \(x=\tfrac{\pi}{2}\).Conceptual Phone a Friend
At \(x=\tfrac{\pi}{2}\), \(\cos x=0\). Compare that with the linear-in-\(x\) term from the polynomial derivative.13. \(f(x)=2e^{x}-5x^{2}+1\)
Follow-up: Find \(f''(x)\), \(f'''(x)\), and \(f^{(4)}(x)\), what will happen if you keep going?
Math Hint
Differentiate term by term.Remember: the derivative of \(e^{x}\) is itself, and powers of \(x\) follow the Power Rule.
Keep track of signs—each new derivative reduces the degree of the polynomial part.
Conceptual Phone a Friend
Notice that the exponential term never disappears under differentiation,while the polynomial part eventually becomes constant and then \(0\).
This highlights the difference between exponential and algebraic growth.
14. \(f(x)=7x^{3}+e^{x}\)
Follow-up: Which term dominates \(f'(x)\) as \(x\to -\infty\)? As \(x\to+\infty\)?
Math Hint
Differentiate to a sum of a polynomial and an exponential. Compare sizes in each limit.Conceptual Phone a Friend
As \(x\to -\infty\), exponentials collapse toward \(0\) while even powers of \(x\) grow large (but positive). As \(x\to+\infty\), exponentials eventually outgrow any polynomial.15. \(f(x)=3\sin x+e^{x}\)
Follow-up: Find \(f''(x)\).
Math Hint
Differentiate term by term: \((\sin x)'=\cos x\) and \((e^{x})'=e^{x}\).Repeat once more to get the second derivative.
Conceptual Phone a Friend
Compare how the exponential and trigonometric parts behave.The exponential term keeps growing, while sine and cosine oscillate between \(-1\) and \(1\).
🔒 Answer Key (Questions 11 – 15)
Click to Unlock Solutions
11.
Derivative: \(f'(x)=6\cos x+3\sin x.\)
Follow-up answer: The equation \(6\cos x+3\sin x=0\) simplifies to \(\tan x=-2\).
Since \(\tan x\) has period \(\pi\), this equality recurs every \(\pi\) units,
so there are infinitely many \(x\) satisfying \(f'(x)=0\).
12.
Derivative: \(f'(x)=8x+3\cos x.\)
Follow-up answer: At \(x=\tfrac{\pi}{2}\), \(f'(x)=8\cdot \tfrac{\pi}{2}+3\cdot 0=4\pi\).
The polynomial term dominates; the trig term contributes \(0\).
13.
First derivative: \(f'(x)=2e^{x}-10x\)
Second derivative: \(f''(x)=2e^{x}-10\)
Third derivative: \(f'''(x)=2e^{x}\)
Fourth derivative: \(f^{(4)}(x)=2e^{x}\)
Follow-up answer:
The exponential term \(2e^{x}\) remains unchanged with each derivative,
while the polynomial part vanishes after two differentiations.
14.
Derivative: \(f'(x)=21x^{2}+e^{x}.\)
Follow-up answer: As \(x\to-\infty\), \(e^{x}\to0\) and \(21x^{2}\) dominates (positive).
As \(x\to+\infty\), both terms increase, but \(e^{x}\) eventually dominates any polynomial.
15.
First derivative: \(f'(x)=3\cos x+e^{x}\)
Second derivative: \(f''(x)=-3\sin x+e^{x}\)
Derivative Applications (Set 4 of 4)
16. \(f(x)=e^{\,5x^{3}+3x-\ln x}\)
Follow-up: Describe what happens to \(f'(x)\) as \(x\) becomes large.
Math Hint
Use the identity\[ \frac{d}{dx}\big(e^{g(x)}\big)=g'(x)e^{g(x)}. \]
First find \(g'(x)\) for \(g(x)=5x^{3}+3x-\ln x\), then look at the signs of \(g'(x)\) and \(e^{g(x)}\) when \(x\) is large.
Conceptual Phone a Friend
Remember that \(e^{g(x)}\) is always positive.If \(g'(x)\) grows quickly and stays positive for large \(x\), then \(f'(x)\) will also grow rapidly.
You’re describing how steeply the function rises for big \(x\).
17. \(f(x)=5\cdot2^{x}+7x^{2}\)
Follow-up: Find \(f''(x)\).
Math Hint
Use the rule \(\dfrac{d}{dx}[a^{x}]=a^{x}\ln a\).Differentiate each term separately; constants stay in front.
Conceptual Phone a Friend
The exponential term keeps its same shape after each derivative,while the polynomial term’s power drops by 1 each time.
18. \(f(x)=4e^{x}-6x^{3}+2\)
Follow-up: Find \(f''(x)\).
Math Hint
Remember: \((e^{x})'=e^{x}\) and constants vanish when differentiated.Apply the Power Rule to \(x^{3}\).
Conceptual Phone a Friend
Each differentiation reduces the power of the polynomial,but the exponential term never changes form.
19. \(f(x)=8x+\log_{10}x\)
Follow-up: Find \(f''(x)\).
Math Hint
Use the base-10 log rule:\[ \frac{d}{dx}[\log_{10}x]=\frac{1}{x\ln10}. \] The linear term’s derivative is just its coefficient.
Conceptual Phone a Friend
The logarithm’s slope decreases as \(x\) grows,while the linear term keeps a constant slope.
20. \(f(x)=3e^{x}+2\ln x\)
Follow-up: Find \(f''(x)\).
Math Hint
Differentiate term-by-term:\((e^{x})'=e^{x}\) and \((\ln x)'=\tfrac{1}{x}\).
Then repeat to get \(f''(x)\).
Conceptual Phone a Friend
Notice how the exponential part keeps increasing at the same rate,but the logarithmic part’s second derivative is negative, showing it bends downward.
🔒 Answer Key (Questions 16 – 20)
Click to Unlock Solutions
16.
Let \(g(x)=5x^{3}+3x-\ln x\).
Then \(g'(x)=15x^{2}+3-\tfrac{1}{x}\).
So
\[
f'(x)=\big(15x^{2}+3-\tfrac{1}{x}\big)e^{\,5x^{3}+3x-\ln x}.
\]
Follow-up answer:
As \(x\) becomes large, \(15x^{2}+3-\tfrac{1}{x}\approx15x^{2}\) (positive and increasing),
and \(e^{\,5x^{3}+3x-\ln x}\) grows extremely fast.
Thus \(f'(x)\) increases rapidly, meaning \(f(x)\) becomes very steep for large \(x\).
17.
First derivative: \(f'(x)=5\cdot2^{x}\ln2+14x\)
Second derivative: \(f''(x)=5\cdot2^{x}(\ln2)^{2}+14\)
18.
First derivative: \(f'(x)=4e^{x}-18x^{2}\)
Second derivative: \(f''(x)=4e^{x}-36x\)
19.
First derivative: \(f'(x)=8+\dfrac{1}{x\ln10}\)
Second derivative: \(f''(x)=-\dfrac{1}{x^{2}\ln10}\)
20.
First derivative: \(f'(x)=3e^{x}+\dfrac{2}{x}\)
Second derivative: \(f''(x)=3e^{x}-\dfrac{2}{x^{2}}\)
10.11 Activity: Reading Math as Instructions — The Product Rule
The Product Rule tells us how to take the derivative of two functions multiplied together.
It’s the mathematical version of saying: “When two things change together, each one’s rate of change contributes to the total change.”
10.11.1 Step 1: Read the Expression Aloud
Prompt:
Read this equation aloud and explain what each part is telling you to do:
\[ \frac{d}{dx}\big[f(x) \cdot g(x)\big] = f'(x)g(x) + f(x)g'(x) \]
| Symbol / Term | What It Tells You To Do |
|---|---|
| \(f(x)\) | |
| \(g(x)\) | |
| \(f'(x)\) | |
| \(g'(x)\) | |
| \(f'(x)g(x) + f(x)g'(x)\) |
Notes:
10.11.2 Step 2: Translate to a Step-by-Step Recipe
Activity (Think–Pair–Share):
Describe the procedure this rule gives you in plain English.
- Identify the two factors — call them \(f(x)\) and \(g(x)\).
- Differentiate the first one (\(f(x)\)) and keep the second one the same.
- Then keep the first one the same and differentiate the second one (\(g(x)\)).
- Add both results together.
Now apply this recipe to a few examples:
| Function \(h(x)\) | \(f(x)\) | \(g(x)\) | \(h'(x)\) |
|---|---|---|---|
| \(x^2 \sin(x)\) | |||
| \(e^x \ln(x)\) | |||
| \((3x-1)(2x^2+5)\) |
Notes:
10.11.3 Step 3: Deriving the Rule from the Limit Definition
If we start from the limit definition of the derivative:
\[ (fg)' = \lim_{h \to 0} \frac{f(x+h)g(x+h) - f(x)g(x)}{h} \]
We can add and subtract \(f(x+h)g(x)\) to rearrange the expression:
\[ (fg)' = \lim_{h \to 0} \frac{f(x+h)g(x+h) - f(x+h)g(x) + f(x+h)g(x) - f(x)g(x)}{h} \]
Group and factor terms:
\[ (fg)' = \lim_{h \to 0} \Big[ f(x+h)\frac{g(x+h)-g(x)}{h} + g(x)\frac{f(x+h)-f(x)}{h} \Big] \]
As \(h \to 0\), the limits become:
\[ \boxed{(fg)' = f'(x)g(x) + f(x)g'(x)} \]
That’s the Product Rule — both parts “help” with the change.
10.11.4 Step 4: Apply the Instructions to a Real Example
Practice:
Let \(f(x) = x^2\) and \(g(x) = \sin(x)\).
Use the Product Rule to find \(\dfrac{d}{dx}\big[f(x)g(x)\big]\).
- Identify \(f(x)\) and \(g(x)\).
- Compute \(f'(x)\) and \(g'(x)\).
- Substitute into \(f'(x)g(x) + f(x)g'(x)\).
- Simplify.
Interpretation (everyday):
Imagine you run a small bakery.
- \(f(x)\) represents how many trays of cookies you bake per hour — your production speed.
- \(g(x)\) represents how many cookies you put on each tray — your batch size.
Your total cookie output per hour is \(f(x) \times g(x)\).
Both of those quantities can change — maybe you’re baking faster as you get into a rhythm,
or maybe you start adding more cookies per tray as demand increases.
The Product Rule tells you how your total production rate changes when both factors are changing at once:
\[ \frac{d}{dx}[f(x)g(x)] = f'(x)g(x) + f(x)g'(x) \]
- The first term, \(f'(x)g(x)\), represents the effect of baking trays faster (speed increasing)
while the number of cookies per tray stays the same.
- The second term, \(f(x)g'(x)\), represents the effect of adding more cookies per tray
while baking speed stays the same.
Together, they show that your total output can rise faster when both your speed and your batch size grow. That’s what the Product Rule captures: two changing things, both contributing to the total change.
Notes:
Interpretation (environmental):
Now imagine an ecosystem instead of a bakery.
- \(f(x)\) represents the amount of plant biomass
— how much living material there is per hectare.
- \(g(x)\) represents the rate of photosynthesis per unit biomass — how productive each unit of plant matter is.
The total carbon fixed per hectare is \(f(x) \times g(x)\).
Both factors can change over time:
- forests grow, increasing total biomass (\(f(x)\) rises), and
- environmental conditions (light, water, temperature) alter photosynthetic efficiency (\(g(x)\) changes).
The Product Rule describes how total carbon uptake changes when both of these processes evolve together:
\[ \frac{d}{dx}[f(x)g(x)] = f'(x)g(x) + f(x)g'(x) \]
- \(f'(x)g(x)\): added carbon uptake because biomass is growing, even if efficiency stays the same.
- \(f(x)g'(x)\): added carbon uptake because each unit of biomass is working harder, even if biomass stays fixed.
Together, these terms explain how ecosystems can accelerate or slow their overall productivity —
it’s not just how much life there is, but also how efficiently that life converts sunlight into energy.
The Product Rule captures how those two changing processes interact to drive total change.
Notes:
10.11.5 Step 5: Reflect — When Two Things Change Together
Reflection Prompt:
Complete this thought:
“When I see \(\frac{d}{dx}[f(x)g(x)] = f'(x)g(x) + f(x)g'(x)\), I think of it as saying ________.”
Notes:
10.12 Activity: Reading Math as Instructions — The Quotient Rule
The Quotient Rule tells us how to take the derivative of one function divided by another.
It’s the mathematical version of saying: “When one changing quantity is divided by another, both affect how fast the ratio itself changes.”
10.12.1 Step 1: Read the Expression Aloud
Prompt:
Read this equation aloud and explain what each part is telling you to do:
\[ \frac{d}{dx}\left[\frac{f(x)}{g(x)}\right] = \frac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^2} \]
| Symbol / Term | What It Tells You To Do |
|---|---|
| \(f(x)\) | |
| \(g(x)\) | |
| \(f'(x)\) | |
| \(g'(x)\) | |
| \(f'(x)g(x) - f(x)g'(x)\) | |
| \([g(x)]^2\) |
Notes:
10.12.2 Step 2: Translate to a Step-by-Step Recipe
Activity (Think–Pair–Share):
Describe the procedure this rule gives you in plain English.
- Identify the top and bottom functions — call them \(f(x)\) (top) and \(g(x)\) (bottom).
- Differentiate the top (\(f'(x)\)) and keep the bottom the same.
- Subtract the top times the derivative of the bottom (\(f(x)g'(x)\)).
- Divide the entire numerator by the square of the bottom, \([g(x)]^2\).
Now apply this recipe to a few examples:
| Function \(h(x)\) | \(f(x)\) | \(g(x)\) | \(h'(x)\) |
|---|---|---|---|
| \(\dfrac{x^2}{\sin(x)}\) | |||
| \(\dfrac{e^x}{x^2}\) | |||
| \(\dfrac{3x^2+1}{2x-5}\) |
Notes:
10.12.3 Step 3: Deriving the Rule from the Product Rule
We can use the Product Rule and the Power Rule to derive the Quotient Rule.
Since dividing by \(g(x)\) is the same as multiplying by \(g(x)^{-1}\):
\[ \frac{f(x)}{g(x)} = f(x)\cdot g(x)^{-1} \]
Differentiate using the Product Rule:
\[ (fg^{-1})' = f'(x)g(x)^{-1} + f(x)(-1)g(x)^{-2}g'(x) \]
Simplify:
\[ \boxed{\frac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^2}} \]
That’s the Quotient Rule — “low d-high minus high d-low, over low squared.”
10.12.4 Step 4: Apply the Instructions to Real Examples
Practice:
Let \(f(x) = x^2\) and \(g(x) = \sin(x)\).
Use the Quotient Rule to find \(\dfrac{d}{dx}\!\left[\dfrac{f(x)}{g(x)}\right]\).
- Identify \(f(x)\) (top) and \(g(x)\) (bottom).
- Compute \(f'(x)\) and \(g'(x)\).
- Substitute into
\[ \frac{d}{dx}\!\left[\frac{f(x)}{g(x)}\right] = \frac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^2} \] - Simplify.
Interpretation (everyday):
Imagine you’re tracking your miles per gallon while driving.
- \(f(x)\) represents miles traveled, which increases over time.
- \(g(x)\) represents gallons of fuel used, which also changes as you drive.
Your fuel efficiency — miles per gallon — is the ratio \(f(x)/g(x)\).
Both the distance and the fuel consumption are changing,
so the rate of change of efficiency depends on how they change relative to each other.
The Quotient Rule tells us exactly how that balance shifts:
\[ \frac{d}{dx}\!\left[\frac{f(x)}{g(x)}\right] = \frac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^2} \]
- The first term, \(f'(x)g(x)\), shows the effect of driving farther while fuel use stays steady.
- The second term, \(f(x)g'(x)\), subtracts the effect of burning fuel faster.
- Dividing by \([g(x)]^2\) keeps everything scaled to “per gallon.”
If you’re traveling more miles but also burning fuel faster, your efficiency might stay flat or drop —
the Quotient Rule captures how competing changes in numerator and denominator interact.
Interpretation (environmental):
Now think about a lake ecosystem where scientists study nutrient efficiency.
- \(f(x)\) represents total biomass (algae and plants) — the numerator.
- \(g(x)\) represents available nutrients (like nitrogen or phosphorus) — the denominator.
The ratio \(f(x)/g(x)\) measures how efficiently the ecosystem turns nutrients into biomass.
Both can change:
- biomass grows as organisms reproduce, and
- nutrient levels fall as they’re consumed.
The Quotient Rule describes how efficiency changes when both processes shift at once:
\[ \frac{d}{dx}\!\left[\frac{f(x)}{g(x)}\right] = \frac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^2} \]
- \(f'(x)g(x)\): efficiency rises because biomass is increasing (numerator growing).
- \(f(x)g'(x)\): efficiency falls because nutrients are being depleted (denominator shrinking).
- Dividing by \([g(x)]^2\) reflects that the smaller the resource pool,
the more sensitive the ratio becomes to change.
This shows why nutrient-use efficiency can fluctuate even if total biomass is steady —
small shifts in either growth or nutrient supply can strongly affect the balance.
Notes:
10.12.5 Step 5: Reflect — “Low d-High Minus High d-Low”
Reflection Prompt:
Complete this thought:
“When I see \(\dfrac{d}{dx}\!\left[\dfrac{f(x)}{g(x)}\right] = \dfrac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^2}\),
I think of it as saying ________.”
Notes:
10.13 Activity: Reading Math as Instructions — The Chain Rule
The Chain Rule tells us how to take the derivative of a composition of functions —
when one function is inside another.
It’s the mathematical version of saying: “When a change depends on something else that’s also changing, the total rate combines both.”
10.13.1 Step 1: Read the Expression Aloud
Prompt:
Read this equation aloud and explain what each part is telling you to do:
\[ \frac{d}{dx}\big[f(g(x))\big] = f'(g(x)) \cdot g'(x) \]
| Symbol / Term | What It Tells You To Do |
|---|---|
| \(f(g(x))\) | |
| \(f'(g(x))\) | |
| \(g(x)\) | |
| \(g'(x)\) | |
| \(f'(g(x)) \cdot g'(x)\) |
Notes:
10.13.2 Step 2: Translate to a Step-by-Step Recipe
Activity (Think–Pair–Share):
Describe the procedure this rule gives you in plain English.
- Identify the outer function \(f(\,\cdot\,)\).
- Identify the inner function \(g(x)\).
- Differentiate the outer function, keeping the inside the same: \(f'(g(x))\).
- Multiply by the derivative of the inner function \(g'(x)\).
Now apply this recipe to a few examples:
| Function \(h(x)\) | Outer \(f(\cdot)\) | Inner \(g(x)\) | \(h'(x)\) |
|---|---|---|---|
| \((3x^2 + 1)^4\) | |||
| \(\sin(5x)\) | |||
| \(e^{x^3}\) |
Notes:
10.13.3 Step 3: Deriving the Rule Conceptually
If \(y = f(u)\) and \(u = g(x)\), then small changes relate as:
\[ \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} \]
That is — a change in \(x\) causes a change in \(u\),
which in turn causes a change in \(y\).
The total effect multiplies these two rates.
This idea gives us:
\[ \boxed{\frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x)} \]
The Chain Rule captures how nested change works — one rate feeding into another.
10.13.4 Step 4: Apply the Instructions to Real Examples
Practice Example 1 — Everyday Context:
Let \(f(u) = u^2\) and \(g(x) = 3x + 2\).
Then \(h(x) = f(g(x)) = (3x + 2)^2\).
\[ h'(x) = f'(g(x)) \cdot g'(x) = 2(3x + 2) \cdot 3 = 6(3x + 2) \]
Interpretation (everyday):
Imagine a conveyor belt feeding into a machine.
- \(g(x)\): how fast the belt moves — converting time to position.
- \(f(u)\): how output depends on belt position — converting position to output.
If the belt speeds up, the output changes faster — not just because the machine reacts,
but because the input itself is changing more quickly.
The Chain Rule captures this change of a change — when one process drives another.
Practice Example 2 — Environmental Context:
Let \(f(T)\) be the rate of photosynthesis depending on temperature,
and \(T(t)\) be the temperature changing over the course of a day.
Then total photosynthesis rate over time is \(f(T(t))\).
The derivative is:
\[ \frac{d}{dt}[f(T(t))] = f'(T(t)) \cdot T'(t) \]
- \(f'(T(t))\): how sensitive photosynthesis is to temperature.
- \(T'(t)\): how quickly the temperature is changing at that time.
Together, they show how rapidly the system’s productivity responds
to both environmental sensitivity and rate of temperature change.
If temperature rises quickly during midday (\(T'(t)\) large) and plants are temperature-sensitive (\(f'(T(t))\) large),
the total rate of change in photosynthesis spikes — a real-world Chain Rule in action.
Notes:
10.14 Implicit Differentiation
The Implicit Differentiation Rule tells us how to find \(\frac{dy}{dx}\) when \(x\) and \(y\) are entangled in the same equation.
It’s the mathematical version of saying: “When two variables change together to maintain a relationship, we can still find how fast one changes relative to the other.”
10.14.1 Step 1: See It — Why Implicit Differentiation Is Needed
Visual Example: The Curve \(x^2 + y^2 = 25\)
Let’s start with a simple relationship:
\[
x^2 + y^2 = 25
\]
This equation defines a circle — all points \((x, y)\) that are 5 units away from the origin.
Notice something important: you can’t write this as a single function \(y = f(x)\) because for most \(x\)-values, there are two possible \(y\)-values (one above, one below the \(x\)-axis).
That’s exactly where implicit differentiation comes in.
We can still find the slope of the curve at any given point — even when \(y\) isn’t isolated.
10.14.2 Step 3: Connect to Real-World Systems
Example — Environmental Relationship
Suppose a forest’s carbon assimilation rate \(A\) depends on both temperature \(T\) and light intensity \(L\):
\[ A(T, L) = k(T - 5)(L - 100) \]
If the system maintains constant assimilation (\(A = A_0\)), then \(T\) and \(L\) must co-adjust to keep that equality true.
Differentiate both sides with respect to \(T\):
\[ k[(L - 100) + (T - 5)\frac{dL}{dT}] = 0 \]
Solve for \(\frac{dL}{dT}\):
\[ \frac{dL}{dT} = -\frac{L - 100}{T - 5} \]
Interpretation:
To keep carbon assimilation constant, light must decrease as temperature increases.
Implicit differentiation captures this interdependence — how one variable’s change must compensate for another’s.
Notes:
10.14.3 Step 4: Reflect — When Two Variables Depend on Each Other
Reflection Prompt:
Complete this thought:
“When I see an equation like \(x^2 + y^2 = 25\),
I think of it as saying ________.”
Notes:
10.14.4 Step 6: Quick Practice — Apply Implicit Differentiation
Differentiate each equation implicitly with respect to \(x\), then solve for \(\frac{dy}{dx}\).
Each problem highlights a slightly different rule (product, chain, exponential, or logarithmic).
5. \(\ln(xy) = x - y\)
\(\frac{dy}{dx} = \, ?\)
Challenge question:
For the curve \(x^2 + xy + y^2 = 7\), find the slope at the point \((2,1)\).
(Hint: use your \(\frac{dy}{dx}\) expression, then substitute.)
Takeaway:
These examples combine multiple differentiation rules — power, product, chain, exponential, and logarithmic — all within one equation.
Implicit differentiation is the glue that connects them, letting you find slopes even when \(y\) can’t be isolated.
10.15 Mixed Rule Practice
How to Approach Mixed-Rule Derivative Problems
When a function combines multiple differentiation rules — product, quotient, chain, and even implicit differentiation — the key is organization, not speed.
Here’s a systematic way to stay in control:
1. Identify the outermost structure first
Before differentiating anything, ask:
> “What is the main operation holding this function together?”
- Is the whole expression a quotient (something divided by something)?
- A product (two factors multiplied)?
- A composition (a function inside another)?
2. Differentiate layer by layer, not all at once
Treat each layer like peeling an onion:
- Apply the outer rule (product, quotient, or chain).
- Pause — identify any new inner functions that appear.
- Then differentiate those carefully before moving deeper.
Example thought process:
> “The outermost layer is a quotient,
> the numerator has a product,
> and one of those products contains a chain rule.”
That’s already your roadmap.
3. Use clear labels for sub-functions
Name inner pieces temporarily:
\[
N(x) = (x^2 + y^3)e^{\sin(x^2)}, \quad D(x) = \sin(\ln((x e^x + 1)^2)).
\]
Then compute \(N'(x)\) and \(D'(x)\) separately.
You’ll make fewer algebraic mistakes and can check each part for correctness.
4. Watch for implicit terms (\(y\))
Whenever \(y\) appears without being defined as a function of \(x\),
remember:
\[
\frac{d}{dx}(y^n) = n y^{n-1} y'.
\]
This keeps your derivative consistent when later solving for \(\frac{dy}{dx}\).
5. Don’t simplify until the end (or at all)
Simplifying while differentiating hides structure and multiplies errors.
Instead:
- Keep parentheses intact.
- Factor only if it clarifies a repeated term.
- Box your final unsimplified result, then simplify only if needed.
6. Build a mental checklist
| Rule | Typical Signal | Inner derivative? | Common pitfall |
|---|---|---|---|
| Product | factors joined by “×” | No | forgetting both parts |
| Quotient | fraction | No | missing a negative |
| Chain | nested parentheses | Yes | dropping inner derivative |
| Implicit | \(y\) terms | Yes | forgetting \(y'\) |
| Exponential / log | powers, \(e^{g(x)}\), \(\ln(g(x))\) | Yes | misusing log base |
1. Product + Chain
Find \(f'(x)\) for
\[
f(x) = x^2 e^{3x+1}.
\]
Solution
We have a product of \(x^2\) and \(e^{3x+1}\).
Use Product Rule: \((uv)' = u'v + uv'\).
2. Quotient + Chain
Find \(f'(x)\) for
\[
f(x) = \frac{\sin(2x)}{x^3 + 1}.
\]
Solution
Apply the Quotient Rule:
\[
\left(\frac{u}{v}\right)' = \frac{u'v - uv'}{v^2}.
\]
\[ \begin{aligned} u(x) &= \sin(2x) &\Rightarrow&\ u'(x) = \cos(2x)\cdot 2 = 2\cos(2x),\\ v(x) &= x^3 + 1 &\Rightarrow&\ v'(x) = 3x^2. \end{aligned} \]
\[ f'(x) = \frac{(2\cos(2x))(x^3+1) - \sin(2x)(3x^2)}{(x^3+1)^2}. \] No simplification required.3. Quotient + Chain
Find \(f'(x)\) for
\[
f(x) = \sin\!\left(\frac{2x}{x^3 + 1}\right).
\]
Solution
We have a chain rule (outer sine) whose inner function is a quotient.
So the Quotient Rule appears inside the chain.
Outer function:
\[
f(x) = \sin(g(x)) \quad \Rightarrow \quad f'(x) = \cos(g(x)) \cdot g'(x).
\]
Inner function:
\[
g(x) = \frac{2x}{x^3 + 1}.
\]
Apply the Quotient Rule to \(g(x)\):
\[
g'(x) = \frac{(2)(x^3 + 1) - 2x(3x^2)}{(x^3 + 1)^2}
= \frac{2x^3 + 2 - 6x^3}{(x^3 + 1)^2}
= \frac{2 - 4x^3}{(x^3 + 1)^2}.
\]
Now combine both results:
\[ f'(x) = \cos\!\left(\frac{2x}{x^3 + 1}\right) \cdot \frac{2 - 4x^3}{(x^3 + 1)^2}. \]
No simplification required.4. Chain + Implicit
Differentiate implicitly: \[ \cos(y) = x^2 + 3y. \]
Solution
Differentiate both sides with respect to \(x\):
\[ \frac{d}{dx}[\cos(y)] = \frac{d}{dx}[x^2 + 3y]. \]
Left side (Chain Rule):
\[
-\sin(y) \cdot y' = 2x + 3y'.
\]
Key takeaway:
Mixed-rule problems aren’t harder because they’re longer —
they’re harder because they require knowing what rule to apply when.
Slowing down and naming each layer keeps everything under control.
Environmental Applications Logistic Growth Model
The logistic growth model describes how a population evolves when growth is limited by resource availability.
1. Population Model
We begin with a population \(P(t)\) that grows over time \(t\), approaching a maximum sustainable size \(K\), called the carrying capacity.
The logistic model expresses this as:
\[ P(t) = \frac{K}{1 + A e^{-rt}}, \]
where:
- \(K\) = carrying capacity
- \(r\) = intrinsic growth rate
- \(A = \frac{K - P_0}{P_0}\), determined by the initial population \(P_0\)
2. Derivative — The Logistic Differential Equation
Differentiating \(P(t)\) with respect to time gives the rate of population change:
\[ \frac{dP}{dt} = rP\!\left(1 - \frac{P}{K}\right). \]
This is the logistic differential equation, which captures the feedback between population size and resource limits.
3. Interpretation
When \(P\) is small, \((1 - P/K) \approx 1\), and growth is approximately exponential: \[ \frac{dP}{dt} \approx rP. \]
As \(P\) increases, \((1 - P/K)\) decreases, slowing growth.
When \(P = K\): \[ \frac{dP}{dt} = 0, \] meaning the population stabilizes at carrying capacity.
4. Growth Phases
| Phase | Condition | Behavior |
|---|---|---|
| Initial | \(P \ll K\) | Nearly exponential growth |
| Midpoint | \(P = \tfrac{K}{2}\) | Maximum growth rate |
| Late | \(P \to K\) | Growth slows and levels off |
5. Key Insight
The logistic model formalizes self-limiting growth: as population size increases, available resources per individual decrease, reducing the overall growth rate.
It serves as the foundation for many ecological and environmental system models.
6. Complex Relationships
Real systems often have parameters that change over time (or with environment).
Below are simple, smooth functions for the logistic model’s parameters and how
they appear when substituted into the population model.
Simple time-varying parameters
Let \[ \begin{aligned} r(t) &= r_0 \;+\; \alpha\sin(2\pi t) \quad &&\text{(seasonal growth rate)},\\[2pt] K(t) &= K_0\!\left[1+\varepsilon\cos(2\pi t)\right] \quad &&\text{(seasonal carrying capacity)},\\[2pt] A(t) &= A_0\!\left[1+\delta e^{-t}\right] \quad &&\text{(transient offset)}. \end{aligned} \]
All amplitudes satisfy \(\alpha,\varepsilon,\delta\ge 0\) and are chosen so \(K(t)>0\) for all \(t\).
Substitution into the population model
The constant-parameter logistic solution is \[ P(t)=\frac{K}{1+A\,e^{-rt}}. \]
\[ P(t)= \frac{K}{1+A\, \exp\!\left( -r_0t-\frac{\alpha}{2\pi}\big(1-\cos(2\pi t)\big) \right)}. \]
🧟 Frankenstein’s Derivative
You’ve learned how the product, quotient, chain, and implicit differentiation rules connect —
now you’ll bring them all together in one (truly monstrous) expression.
Your Task
Find \(f'(x)\) for the following function without simplifying:
\[ f(x)=\frac{(x^2+y^3)e^{\sin(x^2)}}{\sin\!\Big(\ln\!\big((x e^x+1)^2\big)\Big)}. \]
Creating a Solution Path
In a group on the poster paper provided - piece together a solution plan.
- Identify the outermost rule first (which rule applies to the full expression).
- Clearly label inner and outer functions before differentiating each.
- What is your solution route? Which rule to which section first?
- Show every derivative step — you do not need to simplify.
Reflection
After finishing, discuss with your group:
- How many distinct derivative rules were needed?
- What was the “deepest” nesting of rules in your work?
- Where might errors most easily occur — and how can you organize your work to prevent them?
🔒 Frankenstein’s Derivative — Full Solution
Click to Unlock Solution
Step-by-Step Solution (unsimplified)
We start with
\[
f(x)=\frac{(x^2+y^3)e^{\sin(x^2)}}{\sin\!\Big(\ln\!\big((x e^x+1)^2\big)\Big)}.
\]
Step 1 — Outer Rule (Quotient)
\[
f'(x)=\frac{D(x)\,N'(x)-N(x)\,D'(x)}{[D(x)]^2},
\]
where
\(N(x)=(x^2+y^3)e^{\sin(x^2)}\) and
\(D(x)=\sin\!\Big(\ln\!\big((x e^x+1)^2\big)\Big)\).
Step 2 — Differentiate the Numerator \(N(x)\)
Product rule: \(N=u\cdot v\).
\[ u(x)=x^2+y^3 \quad\Rightarrow\quad u'(x)=2x+3y^2y'. \]
\[ v(x)=e^{\sin(x^2)} \quad\Rightarrow\quad v'(x)=e^{\sin(x^2)}\cdot \cos(x^2)\cdot(2x). \]
Combine: \[ N'(x)=\big(2x+3y^2y'\big)e^{\sin(x^2)} + (x^2+y^3)e^{\sin(x^2)}\cos(x^2)(2x). \]
Step 3 — Differentiate the Denominator \(D(x)\)
\[ D(x)=\sin\!\Big(\ln\!\big((x e^x+1)^2\big)\Big) \]
Outer sine ⇒ cosine times derivative of inside:
\[ D'(x)=\cos\!\Big(\ln\!\big((x e^x+1)^2\big)\Big)\cdot \frac{d}{dx}\Big[\ln\!\big((x e^x+1)^2\big)\Big]. \]
Now for the inner log: \[ \frac{d}{dx}\Big[\ln((x e^x+1)^2)\Big] =\frac{1}{(x e^x+1)^2}\cdot \frac{d}{dx}\big[(x e^x+1)^2\big]. \]
Differentiate the square: \[ \frac{d}{dx}\big[(x e^x+1)^2\big] =2(x e^x+1)\cdot \frac{d}{dx}(x e^x+1). \]
Product rule inside: \[ \frac{d}{dx}(x e^x+1)=e^x+x e^x. \]
Assemble: \[ D'(x)=\cos\!\Big(\ln\!\big((x e^x+1)^2\big)\Big)\cdot \frac{2(x e^x+1)(e^x+x e^x)}{(x e^x+1)^2}. \]
Step 4 — Combine Everything
\[ f'(x) = \frac{ \sin\!\Big(\ln\!\big((x e^x+1)^2\big)\Big) \Big[ (2x+3y^2y')e^{\sin(x^2)} +(x^2+y^3)e^{\sin(x^2)}\cos(x^2)(2x) \Big] - (x^2+y^3)e^{\sin(x^2)} \Big[ \cos\!\Big(\ln\!\big((x e^x+1)^2\big)\Big) \frac{2(x e^x+1)(e^x+x e^x)}{(x e^x+1)^2} \Big] }{ \Big[\sin\!\Big(\ln\!\big((x e^x+1)^2\big)\Big)\Big]^2 }. \]
No simplification required.
This is the unsimplified, fully expanded derivative showing all applications of:
- Quotient rule (outermost)
- Product rule (numerator)
- Chain rule (exponentials and trigs)
- Implicit differentiation (via \(y^3 \to 3y^2y'\))
- Nested chain and product rules (in the denominator)